In Part 2 I gave an overview of how two participants of a payment channel go about agreeing on a state and how they update their state. In this post we will look at the scripts used in the commitment transactions and dig into the revocation key process a bit more.
Taking a look at Alice’s commitment transaction again: it spends from the funding transaction and has two outputs: a to_local output and a to_remote output.
to_remote
This output is simply a P2WPKH send to a public key belonging to Bob.
<remotepubkey>
to_local
This output has 2 spending paths:
- the first is to a
<revocationpubkey> - the second is to a Public key belonging to Alice but is only spendable after a relative delay of
to_self_delayblocks.
OP_IF
# Penalty transaction
<revocationpubkey>
OP_ELSE
`to_self_delay`
OP_CHECKSEQUENCEVERIFY
OP_DROP
<local_delayedpubkey>
OP_ENDIF
OP_CHECKSIG
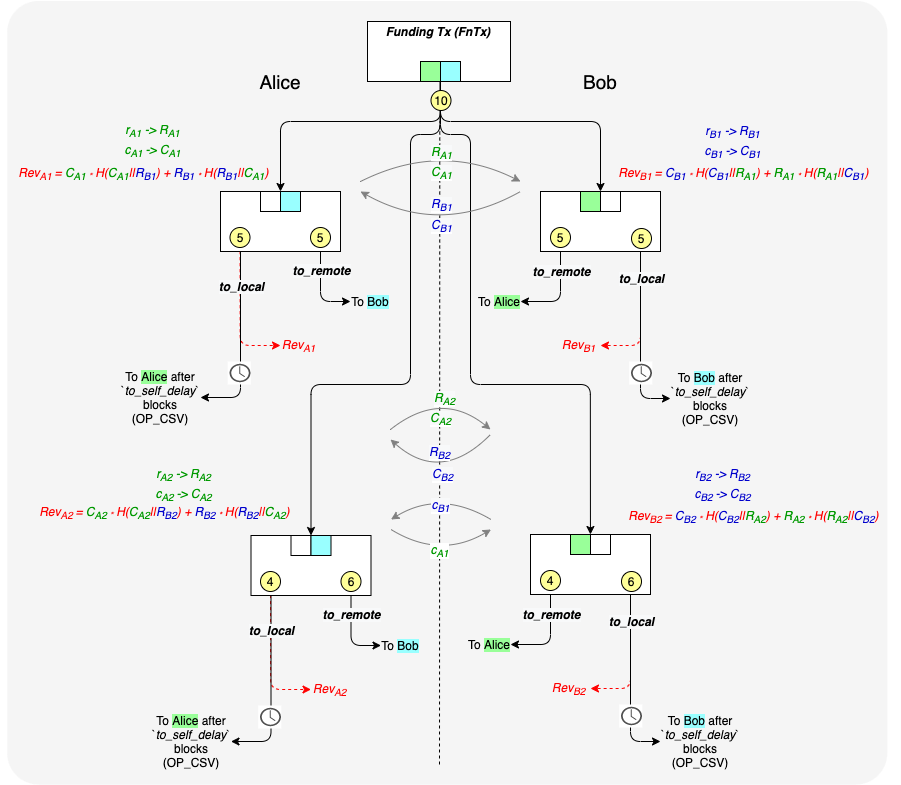
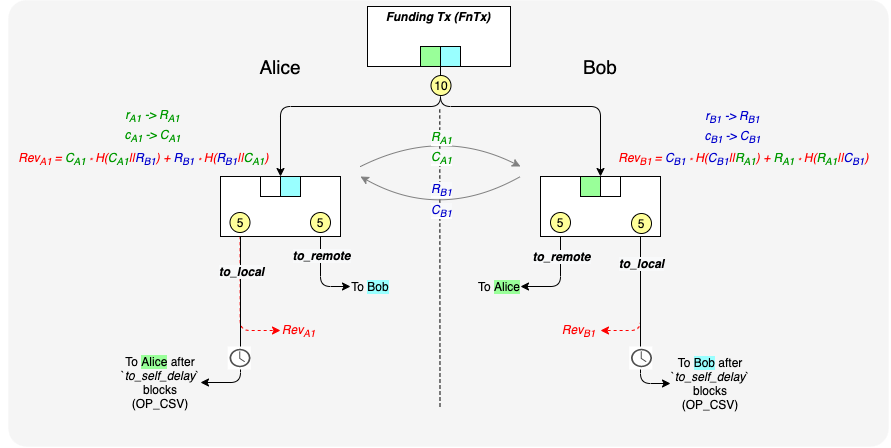
In Part 2, the revocation key system was described as follows:
- Alice generates a temporary private key
dA1and its corresponding public keyPA1and sends the public key to Bob. - Then Alice creates a commitment transaction where the
to_local_outputoutput has a spending path that is immediately spendable by Bob if he has the private ketdA1. - If Alice and Bob agree to update their channel state, then the private keys for the previous state will be swapped (ie: Alice will send Bob
dA1).
This description is mostly correct but not complete. If you take a look at the to_self_delay script above, you can see that the revocation path doesn’t have any condition that makes it seem like only Bob can spend it. It just looks like anyone with the private key corresponding the revocation public key can spend the output. This makes it seem like Alice can also spend the output since she is the one who derived the temporary private key in the first place. After diving into the LND code a bit to try and figure this out, I found that a very cool trick is used to ensure that only Bob can spend via the revocation path. (See function DeriveCommitmentKeys).
Before construction the commitment transactions, both Alice and Bob derive two temporary keys and the associated public keys. They will both derive a revocation_basepoint (r -> R) and a per_commitment_point (c -> C).
- Alice will have her revocation_basepoint key pair:
rA1->RA1and her per-commitment key pair:cA1->CA1. - Bob will have his revocation_basepoint key pair:
rB1->RB1and his per-commitment key pair:cB1->CB1.
Now, in order to create her commitment transaction, Alice will send Bob her commitment point public key, CA1 and Bob will send Alice his revocation_basepoint public key, RB1. Alice then derives the following Revocation key RevA1 as follows:
Rev_A1 = R_B1 * sha256( R_B1 || C_A1 ) + C_A1 * sha256( C_A1 || R_B1 )
Alice’s to_local output script now looks as follows:
OP_IF
<Rev_A1>
OP_ELSE
`to_self_delay`
OP_CHECKSEQUENCEVERIFY
OP_DROP
<alice_delayedpubkey>
OP_ENDIF
OP_CHECKSIG
Now when the times comes for Alice and Bob to update their state and invalidate this old state, Alice sends Bob her private key for her per-commitment key pair, c_A1. With this key, Bob will be able to derive the private key corresponding the the public key Rev_A1 and will therefore be able to spend via the revocation output. He can do this because he has private key r_B1 that corresponds to public key R_B1. So he can calculate the private key as follows:
rev_A1 = r_B1 * sha256( R_B1 || C_A1 ) + c_A1 * sha256( C_A1 || R_B1 )
Alice will not be able to derive this private key because she does not and will never have the private key r_B1.
Updated Diagrams from Post 2:
State 1:
State 2: